Learning-Augmented Algorithms for Boolean Satisfiability

Learning-augmented algorithms are a prominent recent development in beyond worst-case analysis. In this framework, a problem instance is provided with a prediction (``advice'') from a machine-learning oracle, which provides partial information about an optimal solution, and the goal is to design algorithms that leverage this advice to improve worst-case performance. We study the classic Boolean satisfiability (SAT) decision and optimization problems within this framework using two forms of advice. ``Subset advice" provides a random $\epsilon$ fraction of the variables from an optimal assignment, whereas ``label advice" provides noisy predictions for all variables in an optimal assignment. For the decision problem $k$-SAT, by using the subset advice we accelerate the exponential running time of the PPSZ family of algorithms due to Paturi, Pudlak, Saks and Zane, which currently represent the state of the art in the worst case. We accelerate the running time by a multiplicative factor of $2^{-c}$ in the base of the exponent, where $c$ is a function of $\epsilon$ and $k$. For the optimization problem, we show how to incorporate subset advice in a black-box fashion with any $\alpha$-approximation algorithm, improving the approximation ratio to $\alpha + (1 - \alpha)\epsilon$. Specifically, we achieve approximations of $0.94 + \Omega(\epsilon)$ for MAX-$2$-SAT, $7/8 + \Omega(\epsilon)$ for MAX-$3$-SAT, and $0.79 + \Omega(\epsilon)$ for MAX-SAT. Moreover, for label advice, we obtain near-optimal approximation for instances with large average degree, thereby generalizing recent results on MAX-CUT and MAX-$2$-LIN.

Applications of Littlestone dimension to query learning and to compression

In this paper we give several applications of Littlestone dimension. The first is to the model of \cite{angluin2017power}, where we extend their results for learning by equivalence queries with random counterexamples. Second, we extend that model to infinite concept classes with an additional source of randomness. Third, we give improved results on the relationship of Littlestone dimension to classes with extended $d$-compression schemes, proving a strong version of a conjecture of \cite{floyd1995sample} for Littlestone dimension.

Slowly Changing Adversarial Bandit Algorithms are Provably Efficient for Discounted MDPs

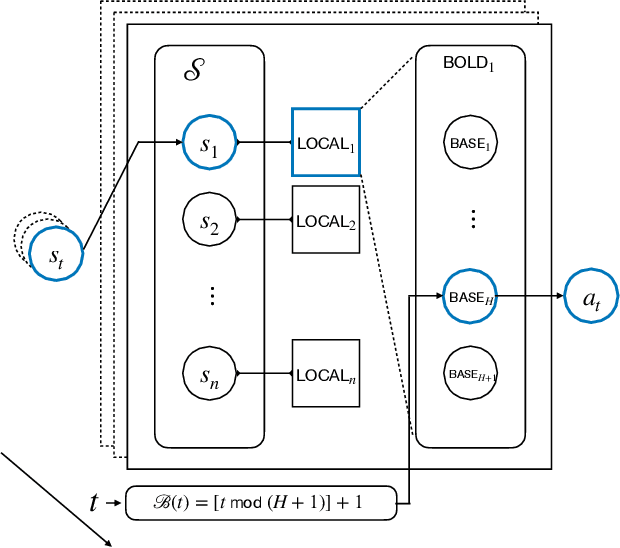
Reinforcement learning (RL) generalizes bandit problems with additional difficulties on longer planning horzion and unknown transition kernel. We show that, under some mild assumptions, \textbf{any} slowly changing adversarial bandit algorithm enjoys near-optimal regret in adversarial bandits can achieve near-optimal (expected) regret in non-episodic discounted MDPs. The slowly changing property required by our generalization is mild, see e.g. (Even-Dar et al. 2009, Neu et al. 2010), we also show, for example, \expt~(Auer et al. 2002) is slowly changing and enjoys near-optimal regret in MDPs.

A Unified Analysis of Dynamic Interactive Learning

In this paper we investigate the problem of learning evolving concepts over a combinatorial structure. Previous work by Emamjomeh-Zadeh et al. [2020] introduced dynamics into interactive learning as a way to model non-static user preferences in clustering problems or recommender systems. We provide many useful contributions to this problem. First, we give a framework that captures both of the models analyzed by [Emamjomeh-Zadeh et al., 2020], which allows us to study any type of concept evolution and matches the same query complexity bounds and running time guarantees of the previous models. Using this general model we solve the open problem of closing the gap between the upper and lower bounds on query complexity. Finally, we study an efficient algorithm where the learner simply follows the feedback at each round, and we provide mistake bounds for low diameter graphs such as cliques, stars, and general o(log n) diameter graphs by using a Markov Chain model.

Communication-Aware Collaborative Learning

Algorithms for noiseless collaborative PAC learning have been analyzed and optimized in recent years with respect to sample complexity. In this paper, we study collaborative PAC learning with the goal of reducing communication cost at essentially no penalty to the sample complexity. We develop communication efficient collaborative PAC learning algorithms using distributed boosting. We then consider the communication cost of collaborative learning in the presence of classification noise. As an intermediate step, we show how collaborative PAC learning algorithms can be adapted to handle classification noise. With this insight, we develop communication efficient algorithms for collaborative PAC learning robust to classification noise.

On the Complexity of Learning from Label Proportions

In the problem of learning with label proportions, which we call LLP learning, the training data is unlabeled, and only the proportions of examples receiving each label are given. The goal is to learn a hypothesis that predicts the proportions of labels on the distribution underlying the sample. This model of learning is applicable to a wide variety of settings, including predicting the number of votes for candidates in political elections from polls. In this paper, we formally define this class and resolve foundational questions regarding the computational complexity of LLP and characterize its relationship to PAC learning. Among our results, we show, perhaps surprisingly, that for finite VC classes what can be efficiently LLP learned is a strict subset of what can be leaned efficiently in PAC, under standard complexity assumptions. We also show that there exist classes of functions whose learnability in LLP is independent of ZFC, the standard set theoretic axioms. This implies that LLP learning cannot be easily characterized (like PAC by VC dimension).

Statistical Queries and Statistical Algorithms: Foundations and Applications

We give a survey of the foundations of statistical queries and their many applications to other areas. We introduce the model, give the main definitions, and we explore the fundamental theory statistical queries and how how it connects to various notions of learnability. We also give a detailed summary of some of the applications of statistical queries to other areas, including to optimization, to evolvability, and to differential privacy.

On Biased Random Walks, Corrupted Intervals, and Learning Under Adversarial Design

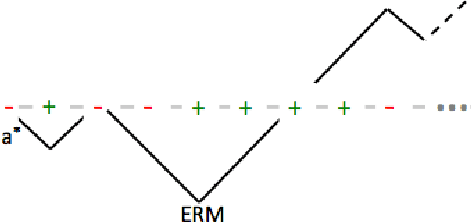
We tackle some fundamental problems in probability theory on corrupted random processes on the integer line. We analyze when a biased random walk is expected to reach its bottommost point and when intervals of integer points can be detected under a natural model of noise. We apply these results to problems in learning thresholds and intervals under a new model for learning under adversarial design.

On Learning a Hidden Directed Graph with Path Queries

In this paper, we consider the problem of reconstructing a directed graph using path queries. In this query model of learning, a graph is hidden from the learner, and the learner can access information about it with path queries. For a source and destination node, a path query returns whether there is a directed path from the source to the destination node in the hidden graph. In this paper we first give bounds for learning graphs on $n$ vertices and $k$ strongly connected components. We then study the case of bounded degree directed trees and give new algorithms for learning "almost-trees" -- directed trees to which extra edges have been added. We also give some lower bound constructions justifying our approach.

Crowdsourced PAC Learning under Classification Noise

In this paper, we analyze PAC learnability from labels produced by crowdsourcing. In our setting, unlabeled examples are drawn from a distribution and labels are crowdsourced from workers who operate under classification noise, each with their own noise parameter. We develop an end-to-end crowdsourced PAC learning algorithm that takes unlabeled data points as input and outputs a trained classifier. Our three-step algorithm incorporates majority voting, pure-exploration bandits, and noisy-PAC learning. We prove several guarantees on the number of tasks labeled by workers for PAC learning in this setting and show that our algorithm improves upon the baseline by reducing the total number of tasks given to workers. We demonstrate the robustness of our algorithm by exploring its application to additional realistic crowdsourcing settings.